贝塞尔曲线

上节课讲解过，threejs 可以通过样条曲线或贝塞尔曲线去表达生活中不规则的曲线，下面给大家介绍贝塞尔曲线有关的知识。

二维二次贝塞尔曲线 QuadraticBezierCurve

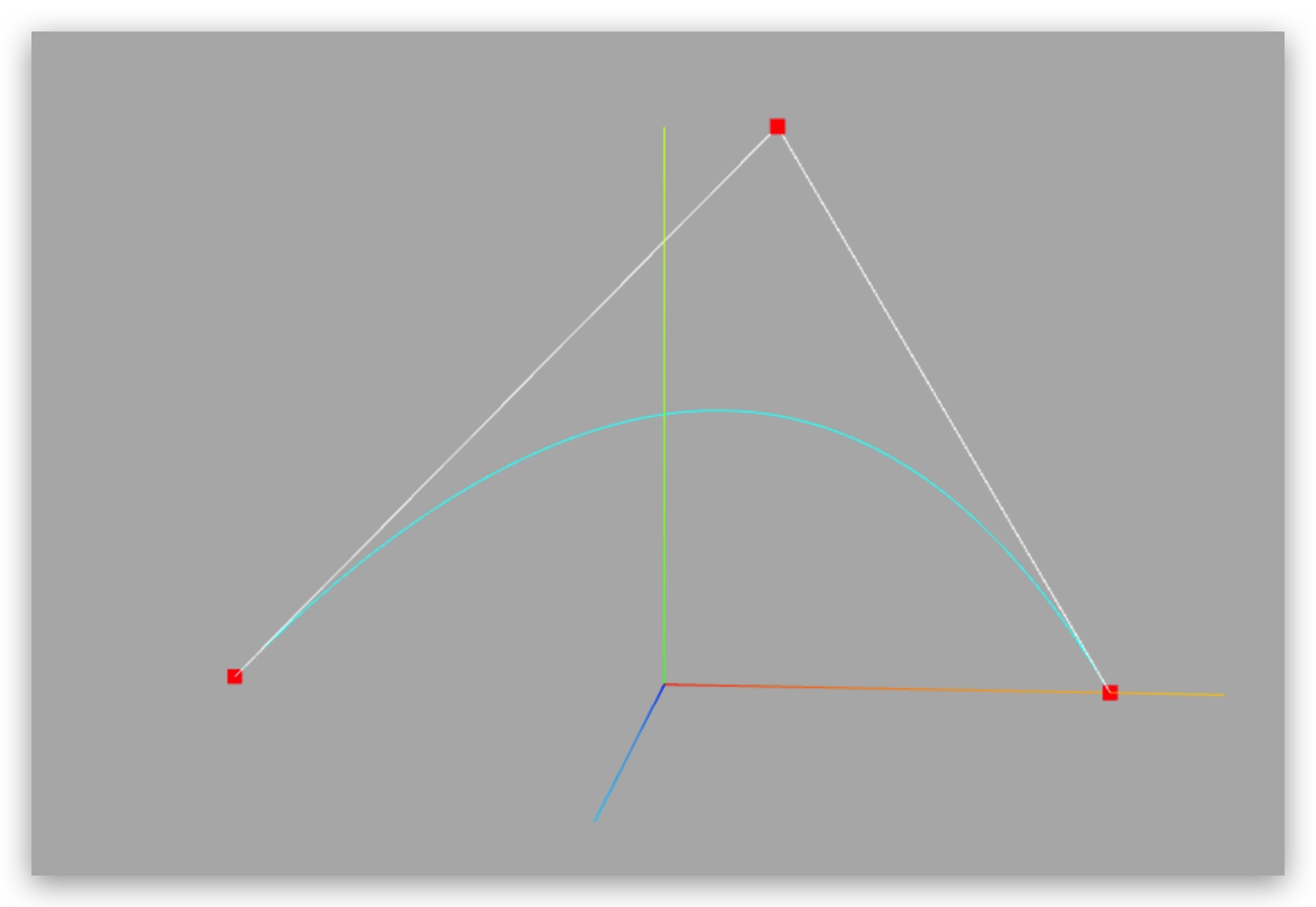
贝塞尔曲线经过 p1、p3 两个点，但是不经过 p2 点，贝塞尔曲线与直线 p12 和 p23 相切。

// p1、p2、p3表示三个点坐标
// p1、p3是曲线起始点，p2是曲线的控制点
const p1 = new THREE.Vector2(-80, 0);
const p2 = new THREE.Vector2(20, 100);
const p3 = new THREE.Vector2(80, 0);

曲线上获取一定数量点，线模型 line 渲染贝塞尔曲线。

// 曲线上获取点
const pointArr = curve.getPoints(50);
const geometry = new THREE.BufferGeometry();
// 读取坐标数据赋值给几何体顶点
geometry.setFromPoints(pointArr);

const material = new THREE.LineBasicMaterial({
  color: 0x00ffff,
});
const line = new THREE.Line(geometry, material);

三维二次贝塞尔曲线 QuadraticBezierCurve3

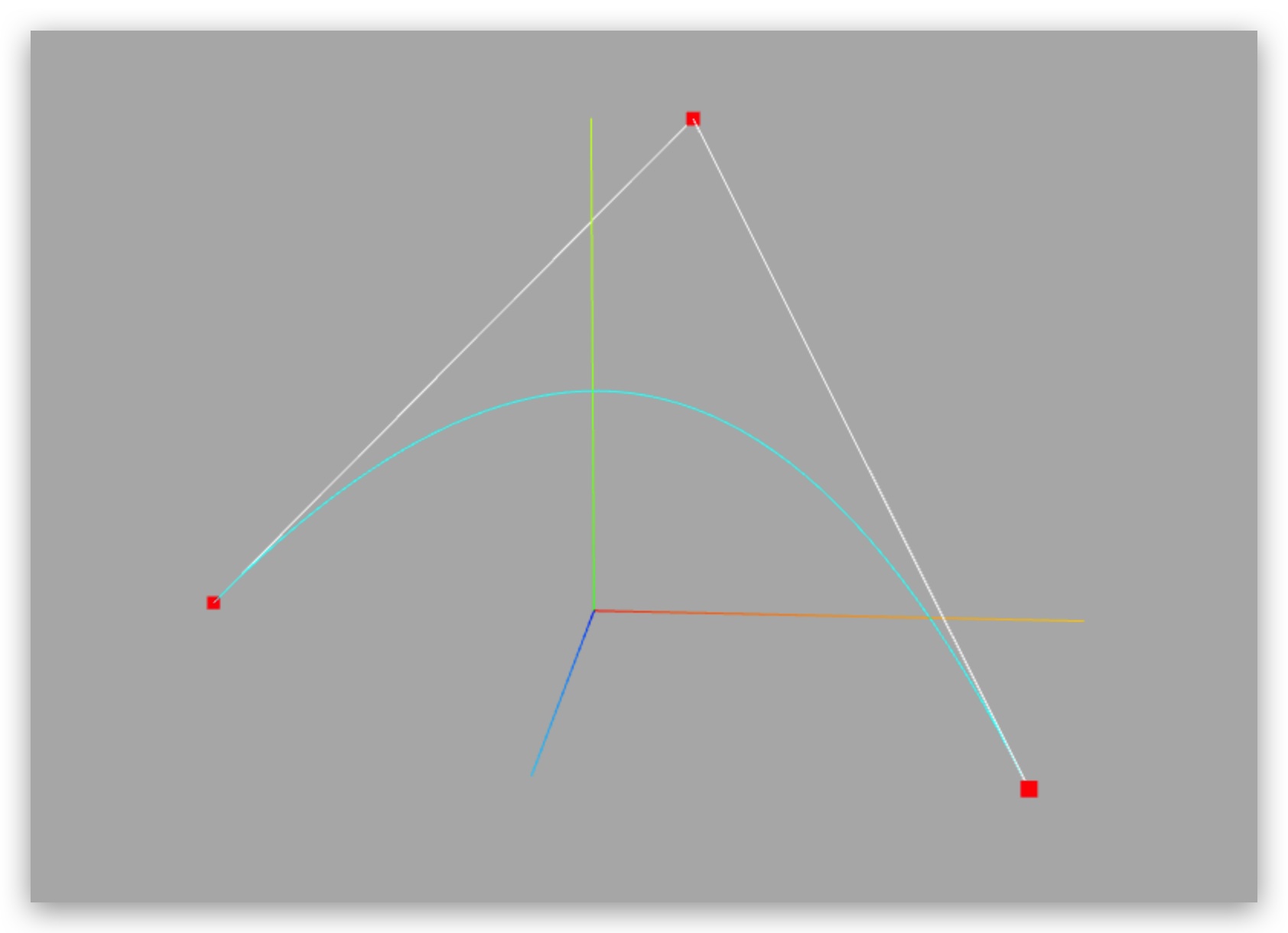
三维二次贝赛尔曲线QuadraticBezierCurve3与二维二次贝赛尔曲线QuadraticBezierCurve区别就是多了一个维度，参数是三维向量对象Vector3。

// p1、p2、p3表示三个点坐标
const p1 = new THREE.Vector3(-80, 0, 0);
const p2 = new THREE.Vector3(20, 100, 0);
const p3 = new THREE.Vector3(80, 0, 100);
// 三维二次贝赛尔曲线
const curve = new THREE.QuadraticBezierCurve3(p1, p2, p3);

二次贝塞尔曲线示例代码

index.vue

代码同 生成圆弧顶点 章节

model.js

import * as THREE from "three";

// p1、p2、p3表示三个点坐标
// p1、p3是曲线起始点，p2是曲线的控制点
// const p1 = new THREE.Vector2(-80, 0);
// const p2 = new THREE.Vector2(20, 100);
// const p3 = new THREE.Vector2(80, 0);

const p1 = new THREE.Vector3(-80, 0, 0);
const p2 = new THREE.Vector3(20, 100, 0);
const p3 = new THREE.Vector3(80, 0, 100);

// 二维二次贝赛尔曲线
// const curve = new THREE.QuadraticBezierCurve(p1, p2, p3);
const curve = new THREE.QuadraticBezierCurve3(p1, p2, p3);

// 获取曲线上的坐标点数量
const pointArr = curve.getPoints(50);

const geometry = new THREE.BufferGeometry();
geometry.setFromPoints(pointArr);

const material = new THREE.LineBasicMaterial({
  color: 0x00ffff,
});

const line = new THREE.Line(geometry, material);

// 用点模型可视化贝塞尔曲线经过的顶点位置
const geometryPoints = new THREE.BufferGeometry();
geometryPoints.setFromPoints([p1, p2, p3]);

const materialPoints = new THREE.PointsMaterial({
  color: 0xff0000,
  size: 10,
});

const points = new THREE.Points(geometryPoints, materialPoints);

// 三个点构成的线条
const line2 = new THREE.Line(geometryPoints, new THREE.LineBasicMaterial());

const group = new THREE.Group();
group.add(line, points, line2);
export default group;

二维三次贝塞尔曲线 CubicBezierCurve

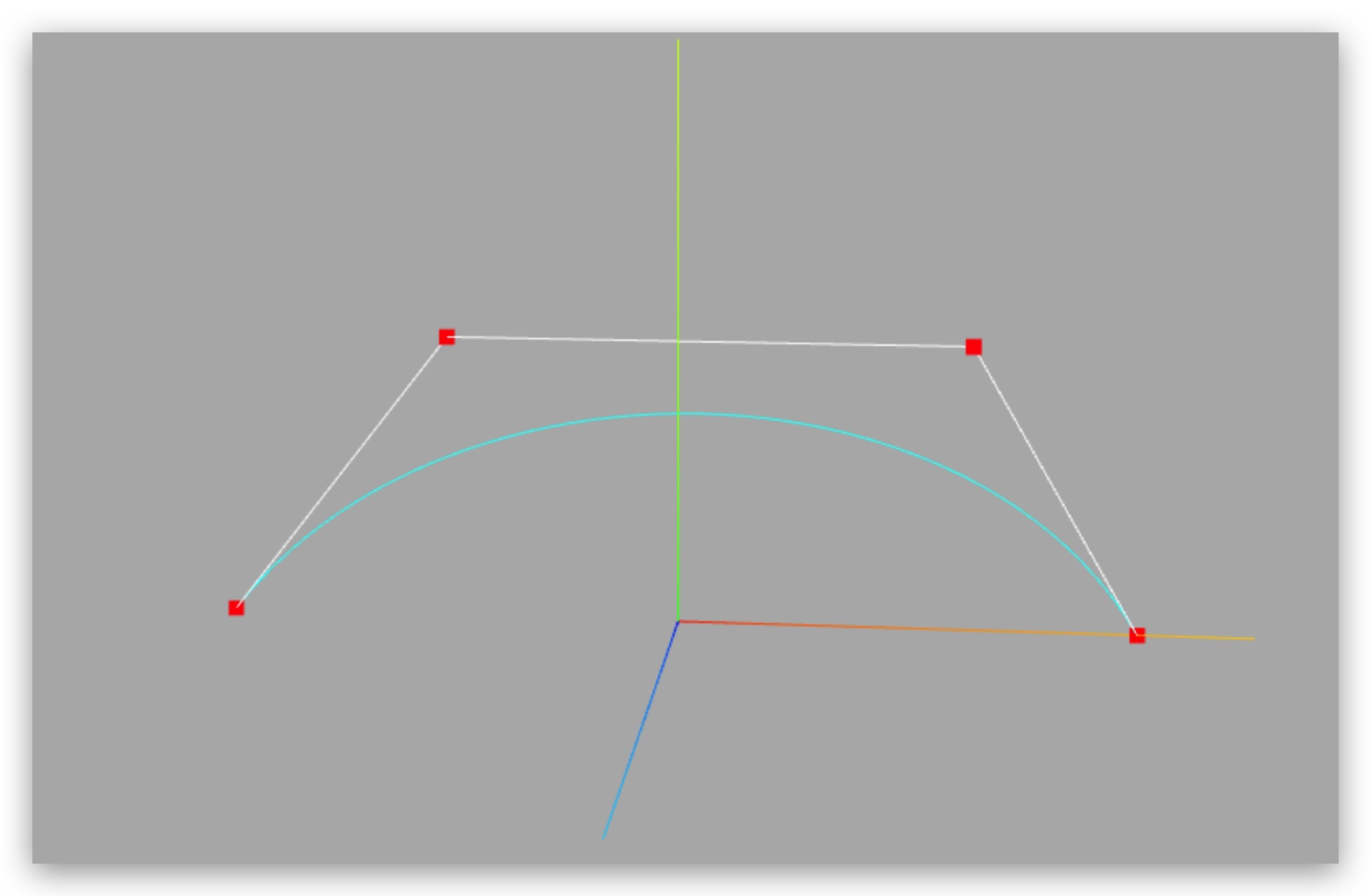
二维三次贝塞尔曲线CubicBezierCurve与二维二次贝赛尔曲线QuadraticBezierCurve区别就是多了一个控制点。

// p1、p2、p3、p4表示4个点坐标
// p1、p4是曲线起始点，p2、p3是曲线的控制点
const p1 = new THREE.Vector2(-80, 0);
const p2 = new THREE.Vector2(-40, 50);
const p3 = new THREE.Vector2(50, 50);
const p4 = new THREE.Vector2(80, 0);

// 二维三次贝赛尔曲线
const curve = new THREE.CubicBezierCurve(p1, p2, p3, p4);

三维三次贝赛尔曲线 CubicBezierCurve3

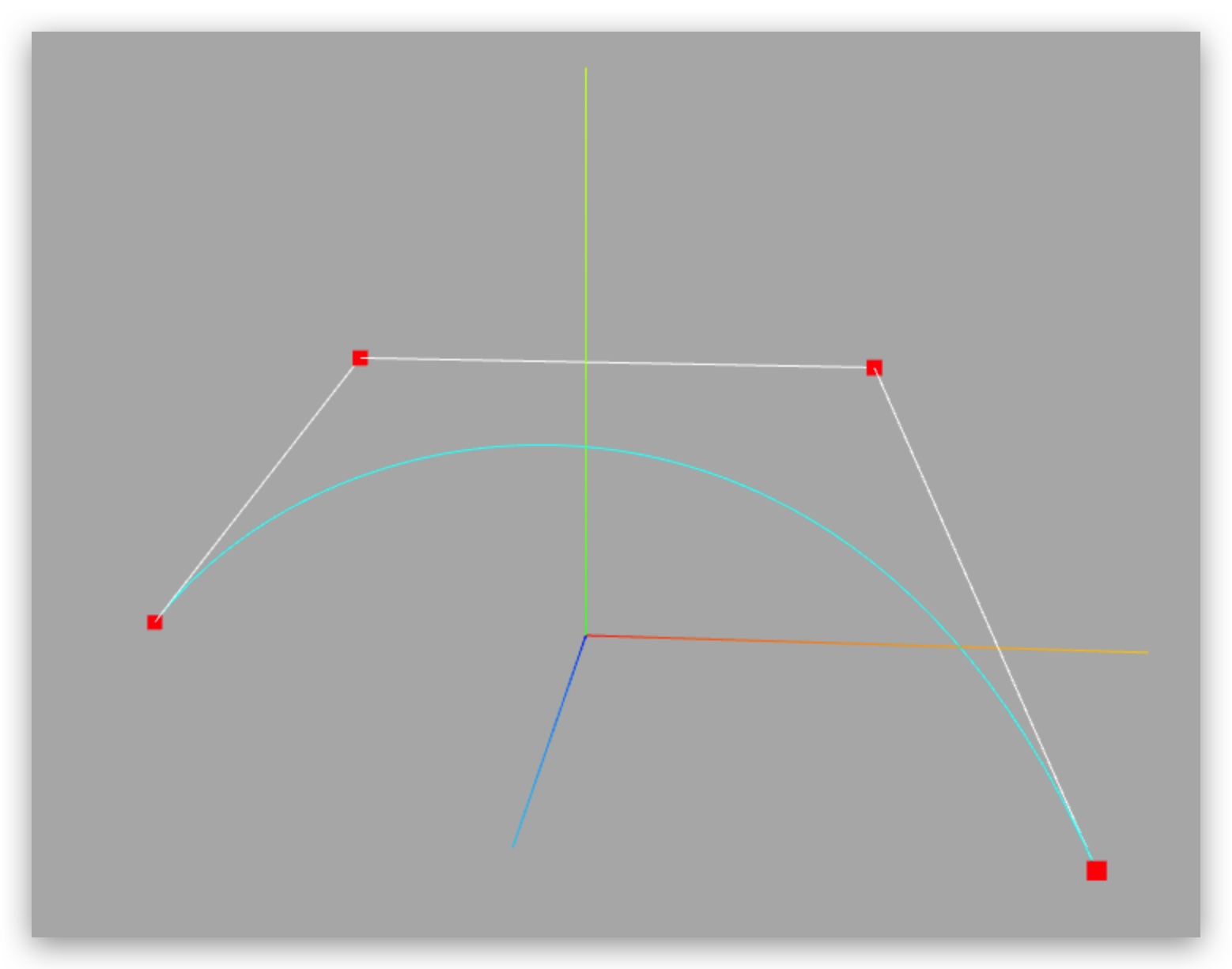
三维三次贝赛尔曲线CubicBezierCurve3与二维三次贝塞尔曲线CubicBezierCurve区别就是多了一个维度，参数是三维向量对象Vector3。

const p1 = new THREE.Vector3(-80, 0, 0);
const p2 = new THREE.Vector3(-40, 50, 0);
const p3 = new THREE.Vector3(50, 50, 0);
const p4 = new THREE.Vector3(80, 0, 100);

// 三维三次贝赛尔曲线
const curve = new THREE.CubicBezierCurve3(p1, p2, p3, p4);

三次贝塞尔曲线示例代码

index.vue

代码同 生成圆弧顶点 章节

model.js

import * as THREE from "three";

// p1、p2、p3、p4表示4个点坐标
// p1、p4是曲线起始点，p2、p3是曲线的控制点
// const p1 = new THREE.Vector2(-80, 0);
// const p2 = new THREE.Vector2(-40, 50);
// const p3 = new THREE.Vector2(50, 50);
// const p4 = new THREE.Vector2(80, 0);

// 二维三次贝赛尔曲线
// const curve = new THREE.CubicBezierCurve(p1, p2, p3, p4);

const p1 = new THREE.Vector3(-80, 0, 0);
const p2 = new THREE.Vector3(-40, 50, 0);
const p3 = new THREE.Vector3(50, 50, 0);
const p4 = new THREE.Vector3(80, 0, 100);

// 三维三次贝赛尔曲线
const curve = new THREE.CubicBezierCurve3(p1, p2, p3, p4);

// 获取曲线上的坐标点数量
const pointArr = curve.getPoints(50);

const geometry = new THREE.BufferGeometry();
geometry.setFromPoints(pointArr);

const material = new THREE.LineBasicMaterial({
  color: 0x00ffff,
});

const line = new THREE.Line(geometry, material);

// 用点模型可视化贝塞尔曲线经过的顶点位置
const geometryPoints = new THREE.BufferGeometry();
geometryPoints.setFromPoints([p1, p2, p3, p4]);

const materialPoints = new THREE.PointsMaterial({
  color: 0xff0000,
  size: 10,
});

const points = new THREE.Points(geometryPoints, materialPoints);

// 三个点构成的线条
const line2 = new THREE.Line(geometryPoints, new THREE.LineBasicMaterial());

const group = new THREE.Group();
group.add(line, points, line2);
export default group;